Золотое сечение — это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве — во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло. Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая — ко всему целому. Приблизительная его величина — 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени. Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом, отражающим структуру и порядок нашего мироустройства.

Пропорция золотого сечения известна людям уже несколько тысяч лет и всё это время не теряет популярности как в чисто математической среде, так и среди художников, скульпторов, философов, биологов. Золотое сечение можно найти в:

• Классической живописи
• Скульптуре
• Архитектуре
• Принципах перспективы и композиции фотографий
• Пропорциях человеческого тела

• Ракушках
• Растениях
• Развитии эмбрионов
• Ветвях галактик
• И во множестве других, подчас весьма необычных, сфер.

Сегодня мы будем говорить о растениях.

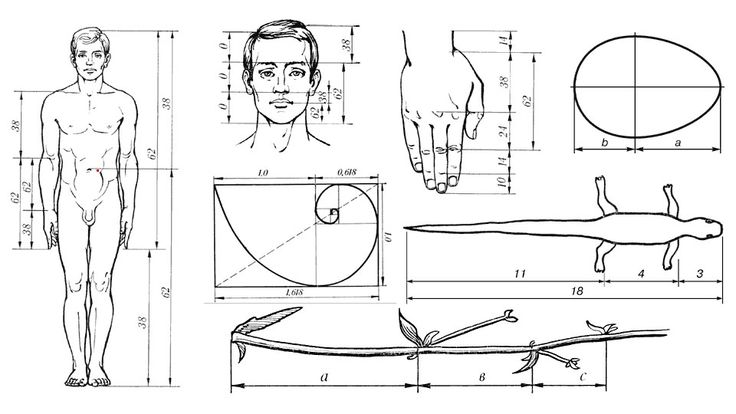
Из труда А. Цезинга “Эстетические исследования”.

 

Идея золотого сечения очень проста. Возьмем отрезок, и разделим его на две части Существует единственный способ разделить отрезок на две части с длинами , так что отношение длины всего отрезка к большей части равно отношению большей части к меньшей. В самом деле, пусть длина отрезка  ; по условию 

Определив  и немного преобразовав систему, получим квадратное уравнение:

У этого уравнения единственный положительный корень

Число  называется числом Фидия или, попросту, пропорцией золотого сечения.

На заглавной картинке изображен цветок подсолнечника маслянистого – растения, масло из семян которого вы почти наверняка регулярно употребляете в пищу. С точки зрения ботаники, большой красивый цветок подсолнуха называется “соцветием-корзинкой”. Желтые лепестки соцветия – видоизмененные листья; они окаймляют корзинку из крошечных желтых цветков, каждому из которых после опыления суждено превратиться в семечко. Рассматривая корзинку подсолнуха, мы можем обнаружить удивительный факт:

 

Человеческий глаз легко различает, как семена группируются по спиралям – левым и правым. Их число различно. Приложив усилия, можно сосчитать, что в цветке подсолнуха на фотографии 21 спираль идет по часовой стрелке и 34 спирали – против часовой. Количества подобных спиралей называются в ботанике парастическими числами (parastichy numbers). Интересно то, что  что близко к . Это не случайно.

Ещё больше примеров парастических чисел

 

Оказывается, у множества видов растений у здорового, неповрежденного цветка или розетки имеется тенденция к выбору в качестве парастических чисел двух соседних чисел следующего ряда:

Эта последовательность широко известна как последовательность Фибоначчи. Она начинается с двух единиц; каждое следующее число последовательности – сумма двух предшествующих. У ряда Фибоначчи много замечательных свойств, главным из которых для нас является то, что отношение двух соседних членов стремится к . Этот замечательный факт напрямую вытекает из явной формулы для чисел ряда Фибоначчи, так называемой формулы Бине:

Как можно видеть, отношение двух соседних членов ряда Фибоначчи быстро стремится в . На самом деле, это характерно для любого рекуррентного ряда, строящегося по формуле “каждый следующий член равен сумме двух предыдущих”.

Откуда же члены последовательности Фибоначчи взялись в цветке?

Процесс формирования корзинки называется филлотаксисом. Внутри центральной части корзинки подсолнуха – меристемы – происходит деление зародышевых клеток, образующих сначала цветок, а потом и семечко. Сразу после рождения цветок начинает выталкиваться младшими братьями и сестрами в радиальном направлении от центра.

Закон движения единичного цветка в корзинке проще всего описать в радиальной системе координат – по радиусу и углу. Для цветка номер  из  рожденных меристемой, его радиальные координаты описываются примерно так:

Помимо  и  мы видим здесь два параметра –  и .  – некая постоянная величина, связанная с размерами цветка в соцветии.

Закон радиального выталкивания легко обосновать физически, приняв за внимание, что цветки соцветия приблизительно одинакового размера и должны покрывать собой всю свободную площадь корзинки. Интереснее закон направления . Он зависит от константы , которая для подсолнуха с высокой точностью равна 

Иными словами, порождая цветок, меристема задает ему направление движения, каждый раз меняя его это направление относительно предшествующего поворотом на .

Примерно таким образом

 

Это число, , неявным образом закодировано в геноме растения. Для того, что бы понять, что это и откуда оно берется, разделим его на , то есть вычислим, какую долю полного оборота оно составляет:

Вот где прячется золотое сечение! Но зачем оно нужно растению?

Для ответа на этот вопрос, обратимся к уникальному свойству числа– его разложению в цепную дробь.

Любое действительное число можно представить следующим способом:

 

Где целое число; прочие натуральные числа. Такое представление называется цепной дробью. Если число – рациональное, его представление в виде цепной дроби насчитывает конечное число членов, и вычисляется посредством алгоритма Евклида. В противном случае, представление числа в виде цепной дроби выражается бесконечной последовательностью знаменателей. Например, знаменитое число  расписывается в виде цепной дроби вот так:

 

Наиболее важным свойством цепных дробей для математики является то, что они кодируют наилучшие рациональные приближения данного числа. В самом деле, попробуем “обрезать” дробь по одной из контурных линий. Мы получим рациональное число, приблизительно равное . Утверждается, что для каждого из них не существует рационального числа с меньшим знаменателем, более близкого к :

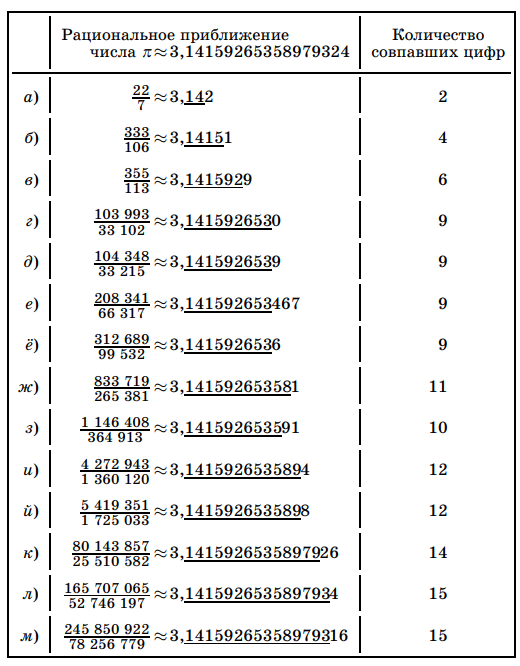
Вычисления взяты из замечательной книжки В. Арнольда “Цепные дроби”

 

Сравните приближение

  и

И в том и в другом случае мы получили 6 значимых цифр после запятой, но в одном случае знаменатель – 113, а в другом – 10000000. Разница, как говорится, налицо.

Теперь, наконец, разложим в цепную дробь. Получится следующее:

Рациональные приближения, полученные посредством обрезания этого представления, выглядят так:

Легко видеть, что это ни что иное, как отношения соседних членов ряда Фибоначчи. И вот теперь, сравнивая цепочку рациональных приближений числа с аналогичной цепочкой числа мы можем видеть главное математическое свойство пропорции золотого сечения.

Для любого достаточно большого , у больше рациональных приближений со знаменателем меньше чем , чем у любого другого иррационального числа.

В самом деле. Приближая , мы видим, что уже у седьмого приближения знаменатель вырос до 99532. Узнаменатель седьмой дроби – 34. Алгоритм вычисления рационального приближения из частичного представления цепной дроби прост, и мы не будем его здесь приводить. Выведя его, легко видеть, что чем меньше числа в ряду, тем меньше будут представления, а натуральных чисел меньше, чем ряд из последовательных единиц, нельзя и представить. Одновременно с этим, является наиболее плохо приближенным числом из всех, в том смысле, что с ростом знаменателя число угаданных знаков приближения растет максимально медленно, насколько это возможно. Этот факт является прямым следствием из теоремы Гурвинца и его доказательство довольно занудно, так что мы не будем включать его в данную статью.

Суха теория, друзья, но древо жизни пышно зеленеет. Настало время сложить всё вышесказанное, и понять, как связаны: филлотаксис подсолнуха, угол , последовательность Фибоначчи, цепные дроби и рациональные приближения. И вместо того, что бы рассказать, лучше показать:

Интерактивное онлайн-демо, иллюстрирующее процесс филлотаксиса

Перейдя по ссылке, вы увидите небольшую онлайн-демонстрацию процесса формирования корзинки подсолнуха. Вы можете регулировать угол порождения меристемой цветков и их количество, или изучать спирали, полученные путем выделения каждого ного зерна, начиная с первого, где n (ранг) – знаменатель одно из рациональных приближений для выставленного вами угла. Вы увидите, что при углах и некоторых других зерна в корзинке распределены почти равномерно, а число рациональных приближений с небольшим основанием максимально; для других углов число рациональных приближений невелико, а зерна подсолнуха четко группируются в спирали, причем их число соответствует знаменателю дроби того или иного рационального приближения выставленного угла. И глядя на это, даже не оперируя сложной математикой вы можете дать правильный ответ на поставленный в заголовке вопрос:

Золотое сечение в подсолнухе обеспечивает наиболее равномерное распределение семян в корзинке за счет наихудшего его приближения рациональными числами и максимизации числа спиралей небольшого ранга, вдоль которых упорядочены семена.

---

Настоящая статья написана по мотивам кружковых занятий Малого Мехмата МГУ для старших классов. В статье использованы следующие источники:

• А. Цезинг “Эстетические исследования”
• В. Арнольд “Цепные дроби”
• А. Щетников “Загадки филлотаксиса” (видео)
• “Математическая составляющая / Филлотаксис” – энциклопедия по популярной математике
• “Special Topics – Lessons from Biology for Engineering Tiny Devices / Lessons 12: Spirals and phyllotaxis” – цикл популярных лекций Принстонского университета, посвященных спиралям.
• Takuya Okabe, Atsushi Ishida and Jin Yoshimura – The unified rule of phyllotaxis explaining both spiral and non-spiral arrangements – более строгое математическое описание процесса развития цветка.
• Математика листьев: как один необычный куст изменил уравнение модели роста растений – статья на habr.com с прелестными анимироваными иллюстрациями.
• Wikipedia: Golden ratio, Continued fraction, Fibonacci number, Hurwitz’s theorem.
• Интерактивное онлайн-демо, иллюстрирующее процесс филлотаксиса

Автор: Антонов Артем
Источник: https://habr.com/