Вычислительная гидродинамика (ВГД) – это раздел науки, решающий проблему моделирования тепломассопереноса в различных технических и природных объектах. Основной задачей ВГД является численное решение уравнений Навье-Стокса, описывающих динамику жидкости. Дополнительно учитываются различные физико-химические эффекты: горение, турбулентность или потоки сквозь пористую среду. Эти уравнения составляют математическую модель тепломассопереноса. ВГД как прикладная наука сформировалась в середине 20 века. Основным потребителем ее результатов была аэрокосмическая промышленность.

С развитием высокопроизводительных компьютеров, которые стали доступны по цене большому числу пользователей, в 70-х годах началось бурное развитие коммерческих программ вычислительной гидродинамики. В 80-х и начале 90-х годов эти программы устанавливаются на компьютеры класса “рабочие станции”. В конце 90-х годов дешевые персональные компьютеры догнали по мощности рабочие станции, а основная операционная система, которая устанавливается на них – MS Windows – стала превосходить по уровню пользовательского интерфейса графические оболочки операционных систем рабочих станций. В это время появились программы в области ВГД, предназначенные для персональных компьютеров.

Вычислительная гидродинамика первоначально развивалась для решения задач аэрокосмической промышленности – расчет камер сгорания ракетных двигателей, расчет физико-химических процессов при обтекании головных частей боеголовок и обтекания сверхзвуковых самолетов.

В настоящее время область применения ВГД значительно расширена гражданскими приложениями. Приведем ниже краткий список задач, решаемых методами ВГД с использованием коммерческих программ.

Автомобильная промышленность: определение коэффициентов сопротивления корпуса автомобиля набегающему воздушному потоку; вентиляция подкапотного пространства и салона; моделирование горения топлива в камере сгорания.

Аэрокосмическая промышленность: моделирование обтекания самолетов и ракет; вентиляция и пожаробезопасность салонов самолетов; моделирование физико-химических процессов в турбореактивных двигателях и в камерах сгорания ракет.

Технологические процессы производства материалов: моделирование литья металлов и пластмасс в форму; моделирование физико-химических процессов в химических и биологических реакторах.

Строительство: расчет ветровых нагрузок на здания и сооружения; вентиляция и пожаробезопасность зданий; определение сопротивлений воздуховодов и водо-раздаточных устройств;

Энергетика: расчет горелок для сжигания топлива в котлах ТЭЦ; расчет выбросов оксидов азота котлами ТЭЦ; определение сопротивлений газоходов;

Экология и чрезвычайные ситуации: моделирования распространения загрязнений в водо-воздушных бассейнах; моделирование распространения пожаров в лесах и городах.

Недавно математики получили более точную (по сравнению с существующими) схему численного решения уравнений Навье — Стокса для плоского течения несжимаемой жидкости. Работа проведена сотрудниками РУДН в соавторстве с российскими и европейскими коллегами. Статья с результатами опубликована в журнале Applied Mathematics and Computation.

Уравнения Навье — Стокса представляют собой систему дифференциальных уравнений, которая позволяет описывать движение вязкой ньютоновской жидкости. Во многих случаях можно пренебречь зависимостью плотности жидкости от координат и времени и считать плотность константой, то есть считать жидкость несжимаемой. С некоторой долей приближения жидкостью Навье — Стокса можно назвать и воду.

Построенная схема позволяет эффективно численными методами решать уравнение для потока несжимаемой жидкости. В работе приводятся расчеты для двумерного движения жидкости (по осям X и Y плюс переменная времени). Это значительно упрощает анализ полученной разностной схемы и работу, так для этого случая известно точное нестационарное решение, и его можно сравнить с результатами, полученными приближенными методами. Путем вычислительных экспериментов и сравнением с точными решениями ученые проверили не только качественно, но и количественно полученную схему численного решения для ламинарного течения жидкости (происходящего без перемешивания ее слоев и пульсаций), не затрагивая турбулентные, в которых образуются вихри и для которых невозможно получить точные решения.

Чтобы решить уравнение численными методами, надо перейти от дифференциальных уравнений к алгебраическим разностным (дискретным) уравнениям.

«Наша задача — построить хорошую схему, которая бы с высокой точностью давала численными методами решение нужной задачи и при этом удовлетворяла ряду специальных свойств, которые накладываются на численные методы», — рассказал математик.

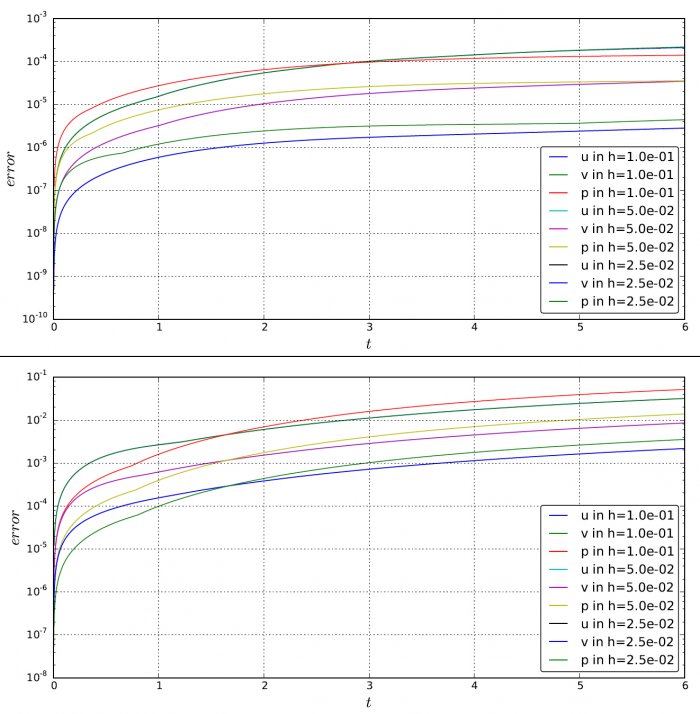Сопоставив свои данные (верхний график) с данными коллег (нижний график), ученые заключили, что их схема имеет примерно на 2 порядка (100 раз) меньшую погрешность и значительно более медленный рост погрешности по времени. Владимир Гердт

«Когда мы задаем начальное условие, удовлетворяющее точечному решению, мы смотрим, как наше численное решение ведет себя во времени, насколько оно будет отклоняться от точного решения. Любой численный метод за счет ошибок и погрешностей всегда отклоняется от точного решения. У других известных и исследованных в работе схем ошибка довольно быстро возрастает во времени, а у нас ошибка очень мала и возрастает очень медленно, это почти константа, — рассказал ученый. — Мы сравнили со стандартными численными методами других авторов и увидели, что наша схема лучше. В этом главный результат работы».

Понравилась статья? Тогда поддержите нас, поделитесь с друзьями и заглядывайте по рекламным ссылкам!