Математики давно пытаются привыкнуть к тому, что некоторые задачи в принципе невозможно решить. Мы любим повторять, что всё возможно. В книге Джастера Нортона «Мило и волшебная будка» король отказывается сообщить Мило, что его цель недостижима, поскольку «многое становится возможным, если не знаешь, что оно невозможно» [правда, это слова других персонажей книги / прим. перев.]. Но в реальном мире некоторые вещи и вправду невозможны, и мы можем доказать это при помощи математики. Люди используют термин «невозможно» разными способами. Он может описывать просто маловероятные вещи – такие, как найти две одинаковых колоды перемешанных карт. Он может описывать задачи, практически невозможные по причине отсутствия времени, места или ресурсов – такие, как переписать всю Библиотеку Конгресса от руки. Устройства типа вечного двигателя невозможны физически, поскольку их существование противоречило бы нашему пониманию физики. Математическая невозможность – это другое. Мы начинаем с недвусмысленных предположений, и, используя математические рассуждения и логику, заключаем, что некоторые исходы событий невозможны.
Никакая удача, настойчивость, время или навыки не сделают задачу выполнимой. История математики полнится доказательствами невозможности. Многие из них считаются наиболее примечательными результатами математики. Но так было не всегда.
Кара за, возможно, самое первое доказательство невозможности, была строгой. Историки считают, что в пятом веке до н.э. Гиппас из Метапонта, последователь Пифагора, обнаружил, что невозможно найти отрезок, которым можно было бы измерить как длину стороны, так и длину диагонали правильного пятиугольника. Сегодня мы говорим, что длина диагонали правильного пятиугольника со стороной длины 1 – золотое сечение, ϕ = 1/2 (1 + √5) – является иррациональным числом. Открытие Гиппаса стало вызовом кредо Пифагора, «всё есть число», поэтому легенды говорят, что Гиппаса либо утопили в море, либо просто изгнали из рядов пифагорейцев.
Более века спустя Евклид возвысил прямую и круг, сочтя их фундаментальными кривыми геометрии. Впоследствии многие поколения геометров чертили всякое – делили углы, проводили перпендикуляры, и так далее – только при помощи циркуля и линейки. Однако определённые конструкции, казавшиеся простыми, поставили греческих геометров в тупик, приобрели в итоге мифический статус, и раздражали математиков более 2000 лет. Это задачи деления произвольного угла на три части, построение стороны куба, объём которого в два раза превышает объём заданного, построение всех правильных многоугольников, а также построение квадрата с площадью, равной площади заданного круга.
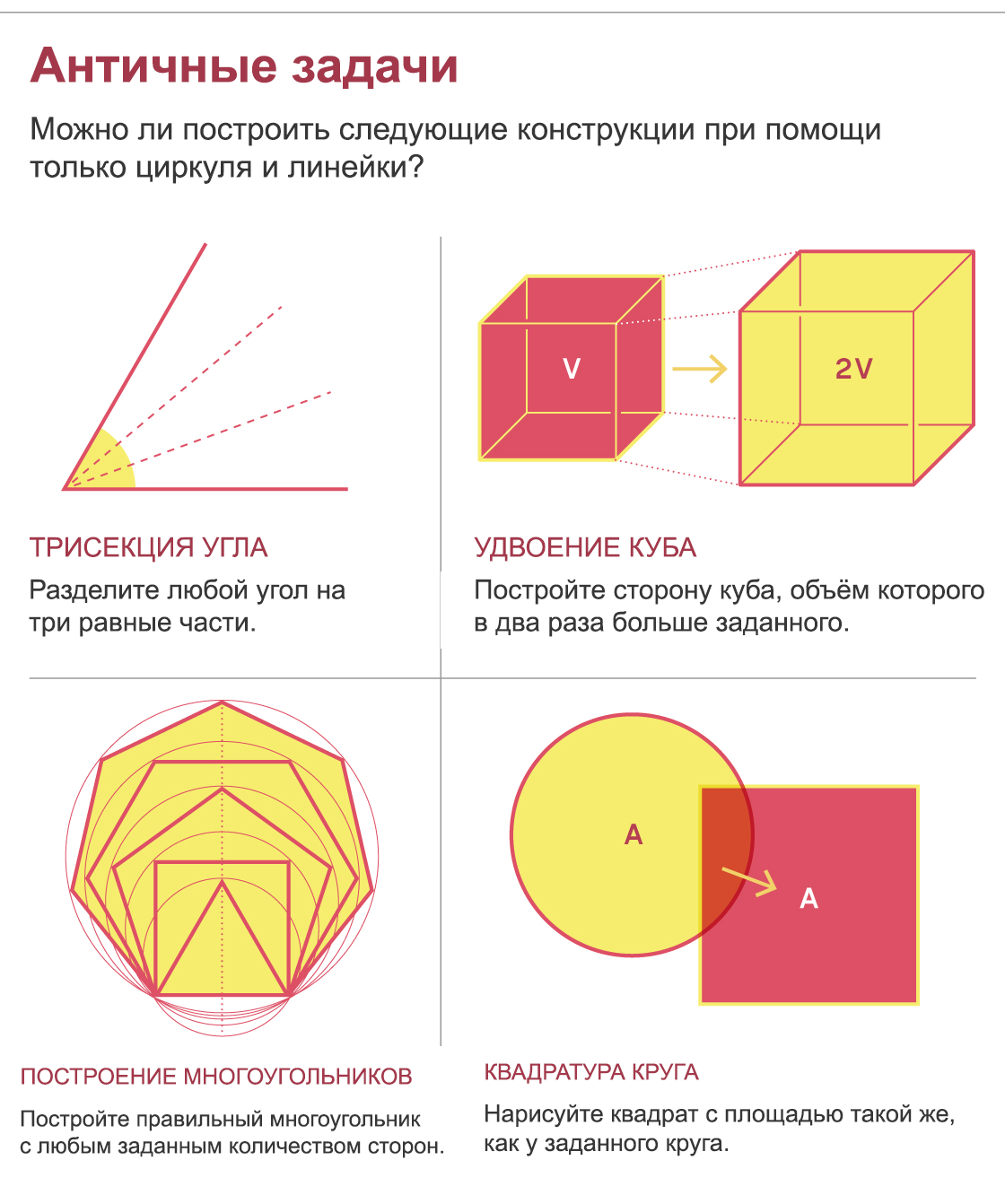
Хотя задачи эти по своей природе геометрические, доказательство невозможности их решения таковым не является. Чтобы продемонстрировать невозможность их решения, потребовалась новая математика.
В XVII века Рене Декарт сделал фундаментальное открытие: если мы ограничим себя только циркулем и линейкой, мы не сможем строить отрезки любой длины. Если мы начнём с отрезка длиной 1, мы сможем строить только такие отрезки, длину которых можно выразить при помощи целых чисел, сложения, вычитания, умножения, деления и извлечения квадратного корня (как золотое сечение).
Поэтому одной из стратегий поиска доказательства невозможности решения геометрической задачи – то есть, что некий объект нельзя построить – будет показать, что длину некоего отрезка итоговой фигуры нельзя выразить указанным способом. Но для того, чтобы это строго показать, потребовалась зарождавшаяся тогда алгебра.
Два столетия спустя соотечественник Декарта, Пьер Лоран Ванцель, использовал многочлены (суммы коэффициентов и переменных, возведённых в степень) и их корни (переменные, при подстановке которых многочлен становится равным нулю) для атаки на эти классические задачи. К примеру, в задаче удвоения куба сторона куба с объёмом, удвоенным по сравнению с объёмом единичного куба, должна быть равной 23. Это корень многочлена x3-2, поскольку (23)3−2=0.
В 1837 Ванцель доказал, что для того, чтобы отрезок можно было построить при помощи циркуля и линейки, его длина должна быть корнем многочлена, который нельзя разложить на множители, и чья степень (наивысшая степень переменной) является степенью двойки. Например, золотое сечение является корнем многочлена второй степени x2 − x − 1. Но x3-2 – это многочлен третьей степени, поэтому 23 построить нельзя. Поэтому Ванцель заключил, что удвоить куб невозможно.
Сходным образом он доказал, что невозможно использовать классические инструменты для трисекции любого угла или построения определённых правильных многоугольников – к примеру, семистороннего. Интересно, что все три доказательства невозможностей были размещены на одной странице. Как у Исаака Ньютона и Альберта Эйнштейна были свои annus mirabilis (годы чудес), так и эту ситуацию можно назвать pagina mirabilis – страницей чудес.
Доказательство невозможности оставшейся задачи, квадратуры круга, потребовала чего-то нового. В 1882 году Фердинанд фон Линдеман доказал ключевой момент – что число π нельзя построить – доказав его трансцендентность, то есть, что оно не является корнем никакого многочлена.
Этим классическим задачам можно приписать дурную репутацию и считать их сиренами, заманивавшими математиков, чтобы те разбивались об острые скалы невозможности. Но я считаю их музами, вдохновлявшими многие поколения творческих мыслителей.
То же касается и более новой невозможной задачи, возникающей из такого простого действия, как переход через мост. Представьте, что вы живёте в Питтсбурге, «городе мостов», как многие из моих учеников. Какой-нибудь велосипедист, любящий приключения, может задуматься – можно ли, начав поездку из дома, проехать ровно один раз по каждому из 22 мостов, пересекающих основные реки Питтсбурга, и вернуться домой.
В 1735 году прусский мэр поставил аналогичную задачу перед Леонардом Эйлером, только для Кёнигсберга (ныне Калининград). Семь мостов этого города объединяют три берега реки и остров. Сначала Эйлер отмёл эту задачу, как не математическую: «Решения такого рода мало связаны с математикой, и я не понимаю, почему вы ожидаете, что его выдаст вам математик, а не кто-либо ещё».
Однако вскоре Эйлер доказал невозможность решения этой задачи, и в процессе создал новую область математики, названную им геометрией расположений – то, что мы сегодня называем топологией. Он понял, что конкретные детали – точные расположения мостов, форма участков земли, и т.п. – были не важны. Важны были только их связи. Позднее математики уточнили формулировки Эйлера с использованием того, что мы сегодня называем графами. Идея связности лежит в основе изучения социальных сетей, интернета, эпидемиологии, лингвистики, планирования оптимальных маршрутов, и т.д.
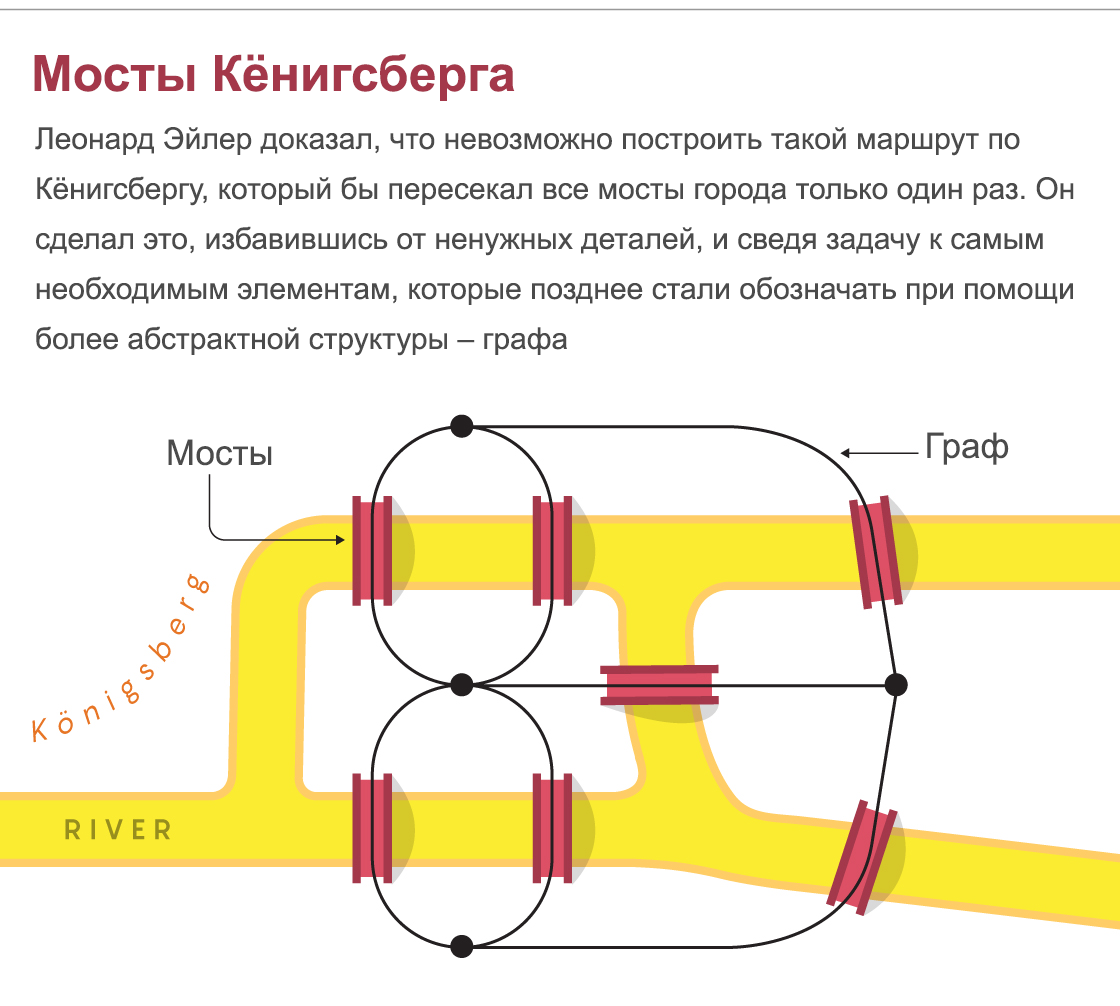Мосты Кёнигсберга: Леонард Эйлер доказал, что невозможно построить такой маршрут по Кёнигсбергу, который бы пересекал все мосты города только один раз. Он сделал это, избавившись от ненужных деталей, и сведя задачу к самым необходимым элементам, которые позднее стали обозначать при помощи более абстрактной структуры – графа.
Доказательство Эйлера было удивительно простым. Он рассудил, что каждый раз, когда мы приходим, а потом уходим с конкретного участка земли, мы должны исключить два моста. Поэтому на каждый участок земли должно вести чётное количество мостов. Но поскольку на каждый участок Кёнигсберга вело нечётное количество мостов, построить такой маршрут было невозможно. Сходным образом три моста, ведущие на остров Герз на реке Аллегейни в Питтсбурге, делают невозможным построение искомого велосипедного маршрута.
Как показывает эта задача, невозможности не ограничиваются абстрактной математикой. У них могут быть последствия и в реальном мире – иногда даже политические.
Недавно математики обратились к такому понятию, как джерримендеринг. В США после каждой переписи штаты должны переделывать избирательные округа. Но иногда правящая партия переписывает их границы смехотворным образом для максимизации своих политических сил.
Во многих штатах есть требование «компактности» округов, не имеющего строгого математического определения. В 1991 году Дэниел Полсби и Роберт Поппер предложили 4πA/P2 в качестве способа измерения компактности округа площади A и периметра P. Эти значения варьируются от 1 для круглого округа до почти нуля у деформированных округов с длинным периметром.
Тем временем Николас Стефанопулос и Эрик Макги ввели в 2014 году понятие «разрыва эффективности» в качестве меры политической честности плана изменения округов. Две разных стратегии джерримендеринга заключаются либо в том, чтобы у оппозиции в округе оказалось менее 50% голосов, или около 100%. Каждая из этих тактик заставляет оппозицию терять голоса, теряя нужных кандидатов, или тратя голоса на тех, кому это не нужно. Разрыв эффективности описывает относительное количество утерянных голосов.
Обе эти меры полезны для распознавания джерримендеринга. Но в 2018 году Борис Алексеев и Дастин Миксон доказали, что «иногда небольшого разрыва эффективности можно достичь при помощи округов странной формы». То есть, математически невозможно всегда рисовать округа так, чтобы они удовлетворяли и требованиям Полсби-Поппера, и честности в плане разрыва эффективности.
Однако обнаружение и предотвращение тайных методов джерримендеринга – это активно развивающаяся область, привлекающая многих талантливых исследований. Как и с проблемами античности или с задачей о мостах Кёнигсберга, я уверен, проблема джерримендеринга вдохновит творческий подход и поспособствует развитию математики.
Автор: Вячеслав Голованов
Источник: https://habr.com/
Понравилась статья? Тогда поддержите нас, поделитесь с друзьями и заглядывайте по рекламным ссылкам!
